Apunte: Estructura de Control Alternativa

1. Introducción

Las alternativas son partes de nuestra vida cotidiana, continuamente lidiamos con ellas en nuestras actividades. Por ej una alternativa como: ’si llueve voy al cine, si no llueve voy a la plaza’, o una alternativa mas trascendental ’¿que carrera voy a seguir?’.

Las estructuras alternativas son una estructura de control útil cuando nos encontramos con problemas que requieren ejecutar una o más instrucciones según diferentes casos. En otras palabras, las estructuras alternativas bifurcan o dirigen la ejecución de un programa hacia un grupo de sentencias u otro dependiendo de una condición. Las distintas condiciones que incluye una alternativa pueden estar explícitas en el mismo problema que debemos resolver por ej: ’dado un entero ingresado por el usuario si el valor del entero es par incrementarlo, si es impar decrementarlo’, o pueden ser parte de la solución matemática o lógica de un problema. Veremos a continuación un ejemplo introductorio a las estructuras alternativas.

2. Alternativas Simples

Imaginemos que tenemos que resolver el siguiente problema:

Problema 1: Debemos leer un número y, si el número es positivo, debemos escribir en pantalla el cartel ” y es un Numero positivo”.

Solución: Especificamos nuestra solución: se deberá leer un número x. Si x > 0 se escribe el mensaje ”Número positivo”. Diseñamos nuestra solución:

ALGORITMO esPositivo() RETORNA ∅
    (* Determina si un entero es positivo *)
    ENTERO x
    ESCRIBIR (”Ingrese un numero entero”)
    LEER(x)
    SI ( x > 0 ) ENTONCES
            ESCRIBIR(x + ”Es un Numero Positivo”)
    FIN SI
FIN ALGORITMO esPositivo

Es claro que la primera línea se puede escribir en JAVA como

Scanner sc = new Scanner(System.in);
x = sc.nextInt();

Sin embargo, con las instrucciones que vimos hasta ahora no podemos tomar el tipo de decisiones que nos planteamos al final del pseudocódigo. Para resolver este problema introducimos una nueva instrucción que llamaremos alternativa o condicional que tiene la siguiente forma:

if ( x > 0 )
  System.out.println(x+” e s un número POSITIVO”);

Donde if es una palabra reservada.

¿De qué tipo es la condición que aparece luego de la palabra reservada if ? Es de tipo LÓGICO ó Booleano. Es decir la evaluación de la expresión arroja un resultado VERDADERO (TRUE) ó FALSO (FALSE). En otras palabras es una expresión booleana.

2.1 Alternativa simple en JAVA

ALGORITMO esPositivo() RETORNA ∅
    (* Determina si un entero es positivo *)
    ENTERO x
    ESCRIBIR (”Ingrese un numero entero”)
    LEER(x)
    SI ( x > 0 ) ENTONCES
            ESCRIBIR(x + ”Es un Numero Positivo”)
    FIN SI
FIN ALGORITMO esPositivo

public class PrimerPrograma
{
// Parte principal de programa
public static void main( String[] args )
{
  // Declaración de variables
  Scanner sc = new Scanner(System.in);
  int x;
  // ingreso de datos
  System.out.println(”Ingrese un número entero”) ;
  x = sc.nextInt();
  // Mostramos por pantalla resultados
  if (x > 0)
      System.out.println(valor+” es POSITIVO”) ;
}

3. Repaso de Expresiones Booleanas

Recordemos que a nivel de diseño contamos con el tipo de dato LOGICO, que contiene solo dos valores: TRUE y FALSE para representar los valores de verdad verdadero y falso respectivamente. Estos valores son los únicos valores del Tipo LOGICO.

El tipo de dato LOGICO se modela en Java con el tipo boolean Vimos que una expresión nos permite producir o calcular un valor (resultado). Una expresión booleana o expresión lógica es una expresión que tiene como resultado TRUE o FALSE.

3.1. Expresiones de comparación

En el ejemplo que queremos resolver, la condición que queremos ver si se cumple o no es que x sea mayor que cero. Para ello, es necesario utilizar un operador de comparación para comparar valores entre sí. En particular la pregunta de si x es mayor que cero, se codifica en Java como x > 0.

De esta forma, 5 > 3 es una expresión booleana cuyo valor es True, y 5 < 3 también es una expresión booleana, pero su valor es False. Otros operadores de comparación en pseudocódigo y en Java son los que se detallan a continuación.

Expresión Pseudocódigo	Expresión Java	Significado
\(a <> b\), \(a \ne b\) \(a= b\) \(a < b\) \(a <= b\) \(a > b\) \(a >= b\)	\(a != b\) \(a == b\) \(a < b\) \(a <= b\) \(a > b\) \(a > b\)	\(a\) es distinto de \(b\) \(a\) es igual a \(b\) \(a\) es menor que \(b\) \(a\) es menor o igual que \(b\) \(a\) es mayor que \(b\) \(a\) es mayor o igual que \(b\)

3.2. Operadores lógicos

De la misma manera que se puede operar entre números mediante las operaciones de suma, resta, etc., también existen tres operadores lógicos para combinar expresiones booleanas: and (y), or (o), not (no) y xor (x-or).

El significado de estos operadores es igual al del castellano, pero vale la pena recordarlo en Tabla II:

Pseudocódigo	Java	Significado
\(a\) AND \(b\),\(a \wedge b\) \(a\) OR \(b\),\(a \vee b\) \(a\) XOR \(b\) \(a\) NOT \(b\)	\(a\) && \(b\) \(a \| b\) \(a \hat{} b\) ! \(a\)	El resultado es TRUE si a es TRUE y b es TRUE de lo contrario el resultado es FALSE El resultado es TRUE si a es TRUE o b es TRUE de lo contrario el resultado es FALSE El resultado es TRUE si a es FALSE de lo contrario el resultado es FALSE El resultado es TRUE si a es False y b es TRUE, o viceversa

Ejemplos: * \(a\) > \(b\) and \(a\) > \(c\) es verdadero si \(a\) es simultáneamente mayor que \(b\) y que \(c\). * \(a\) > \(b\) or \(a\) > \(c\) es verdadero si \(a\) es mayor que \(b\) o \(a\) es mayor que \(c\). * not (\(a\) > \(b\)) es verdadero si \(a\) > \(b\) es falso (o sea si \(a\) <= \(b\) es verdadero)

4. Alternativas Dobles

Problema: En la etapa de mantenimiento nos dicen que, en realidad, también se necesitaría un mensaje Numero no positivo cuando no se cumple la condición.

Modificamos la especificación del algoritmo y del código Java:

ALGORITMO esPositivo() RETORNA ∅
    (* Determina si un entero es positivo *)
    ENTERO x
    ESCRIBIR (”Ingrese un numero entero”)
    LEER(x)
    SI ( x > 0 ) ENTONCES
        ESCRIBIR(x + ”Es un Numero Positivo”)
    SINO
        ESCRIBIR(x + ”No es un Numero Positivo”)
    FIN SI
FIN ALGORITMO esPositivo

public class PrimerPrograma
{
// Parte principal de programa
public static void main( String[] args )
{
  // Declaración de variables
  Scanner sc = new Scanner(System.in);
  int x;
  // ingreso de datos
  System.out.println ( ”Ingrese un número entero” ) ;
  x = sc.nextInt();
  // Mostramos por pantalla resultados
  if (x > 0)
      System.out.println(valor+” es POSITIVO”) ;
  else
      System.out.println(valor+” NO es POSITIVO”) ;
}

En pseudocódigo una alternativa doble se modela de la siguiente forma:

ALGORITMO nombreAlgoritmo() RETORNA ∅
    (* .... *)
    SI ( expresiónBooleana ) ENTONCES
        Bloque de Sentencias a ejecutar si la expresión booleana es TRUE
    SINO
        Bloque de Sentencias a ejecutar si la expresión booleana es FALSE
    FIN SI
    ....
FIN ALGORITMO nombreAlgoritmo

Su significado es el siguiente: se evalúa la ( expresiónBooleana ), si el resultado es TRUE (verdadero) se ejecutan las acciones indicadas en “Bloque de Sentencias a ejecutar si la expresión booleana es TRUE”, y si el resultado es FALSE (falso) se ejecutan las acciones indicadas en “Bloque de Sentencias a ejecutar si la expresión booleana es FALSE”.

En Java para implementar una alternativa doble utilizamos las palabras reservadas: if y else. Si alguno de los bloques de sentencias tiene más de una instrucción es obligatorio encerrar el bloque con llaves.

En una instrucción alternativa doble estamos implementando la operación:
( expresiónBooleana ) ⊕ not ( expresiónBooleana ) donde ⊕ es la notación universal del operador XOR. El operador XOR representa la disyunción exclusiva. Debemos ser conscientes que el diseño de estructura alternativa que modelemos debe representar un XOR. En el pseudocódigo el símbolo ⊕ esta modelado por la palabra reservada SINO

5. Alternativas en la Etapa de Análisis

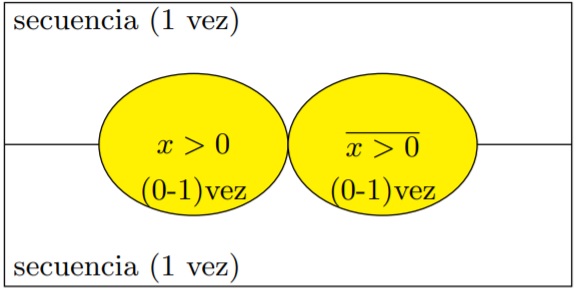
Un conjunto de datos es de estructura alternativa si el mismo constituye un conjunto de datos en el cual se encuentran uno o varios subconjuntos. Cada subconjunto es de presencia aleatoria (condicional), con la salvedad de que la presencia de uno excluye la de todos los demás. Por esta razón, utilizaremos la notación de ⊕ para representar la presencia exclusiva en las expresiones booleanas que representan los distintos tratamientos de conjuntos de información.

Modelamos este tratamiento de datos en la etapa de análisis utilizando conjuntos. La etiqueta (0-1) veces, modela la presencia aleatoria del subconjunto

6. Alternativas en la Etapa de Diseño

Es importante darnos cuenta que en una estructura de datos secuencial todas las sentencias de un bloque son ejecutadas en secuencia. En el caso de una estructura alternativa doble el flujo de ejecución ejecuta diferentes grupos de sentencias dependiendo del valor de la expresión booleana. Es útil mostrar como se modela una estructura alternativa a partir de diagramas de flujo, porque ellos muestran explícitamente el flujo de ejecución. En este tipo de diagramas los bloques secuenciales son mostrados en rectángulos y las expresiones booleanas a partir de rombos.

Los rombos muestran claramente las decisiones tomadas y como el flujo del programa se bifurca. Si la evaluación de la expresión booleana se evalúa a verdadero se ejecuta la secuencia de sentencias de la izquierda (graficado con un rectángulo de puntas redondeadas), si la expresión booleana se evalúa a falso se ejecuta la secuencia de sentencias de la derecha.

La expresión booleana se muestra a partir de un rombo y permite determinar la condición que seleccionará una secuencia de sentencias u otra. Los diagramas de flujo emplean notación gráfica. Sin embargo resulta engorroso leer un diagrama de flujo que modele el diseño de un algoritmo con varias estructuras de control combinadas.

Ahora observemos el flujo de datos de una alternativa doble. A continuación mostramos un diagrama de flujo para el último pseudocódigo que mostramos anteriormente:

Veamos como se distingue una alternativa simple de una alternativa doble segun el flujo de datos. Observemos primero el flujo de datos de una alternativa simple:

7. Múltiples Alternativas combinadas

La decisión de incluir una alternativa en un programa, parte de una lectura cuidadosa de la especificación. En nuestro caso la especificación nos decía: Si el número es positivo escribir un mensaje Numero positivo, de lo contrario escribir un mensaje Numero no positivo. Veamos qué se puede hacer cuando se presentan tres o más alternativas.

Problema: Si el número es positivo escribir el mensaje Numero positivo, si el número es igual a 0 escribir el mensaje Igual a 0 , y si el número es negativo escribir el mensaje ”Número negativo”. Una posibilidad es considerar que se trata de una estructura con dos casos como antes, sólo que el segundo caso es complejo (es nuevamente una alternativa):

ALGORITMO esPositivo() RETORNA ∅
  (* Determina si un entero es positivo,
       igual a cero ó negativo *)
  ENTERO x
  ESCRIBIR (”Ingrese un numero entero”)
  LEER(x)
  SI (x > 0) ENTONCES
      ESCRIBIR(”Número POSITIVO”)
  SINO
      SI ( x = 0 ) ENTONCES
          ESCRIBIR(”Número IGUAL A CERO”)
      SINO
          ESCRIBIR(”Número NEGATIVO”)
      FIN SI      
  FIN SI
FIN ALGORITMO esPositivo

public class PrimerPrograma
{
// Determina si un entero es positivo, igual a cero ó negativo
public static void main( String[] args )
{
  // Declaración de variables
  Scanner sc = new Scanner(System.in);
  int x;
  // ingreso de datos
  System.out.println(”Ingrese un número entero”);
  x = sc.nextInt();
  // Mostramos por pantalla resultados
  if ( x > 0 )
    System.out.println(x +” es POSITIVO”) ;
  else
      if (x==0)
        System.out.println(x+ ” es CERO”) ;
      else
        System.out.println(x+” es NEGATIVO”) ;
}

Esta estructura se conoce como alternativas anidadas ya que dentro de una de las ramas de la alternativa (en este caso la rama del else) se anida otra alternativa. Pero ésta no es la única forma de implementarlo. Existe otra construcción, equivalente a la anterior pero que no exige indentaciones cada vez mayores en el texto. Se trata de la estructura selectiva ó alternativas múltiples.

8. Estructuras Selectivas

Cuando las estructuras anidadas se refieren al tratamiento del mismo subconjunto de datos, y estos subconjuntos son de presencia aleatoria y disjuntos entre sí, es posible modelarlos empleando un mecanismo de abreviación.. Esto es posible si las estructuras anidadas utilizan el mismo conjunto de variables en sus expresiones booleanas (en el pseudocódigo notar que las expresiones booleanas de las estructuras alternativas anidadas operan sobre la variable x). Con frecuencia aparecen problemas donde necesitamos realizar diferentes acciones dependiendo de distintos valores (una cantidad finita) que asume una variable. En estos casos debemos implementar diferentes acciones de acuerdo a la evaluación de una expresión multivaluada.

Por ejemplo, veamos el siguiente problema: Problema: Se desea diseñar un módulo que dado el número de día de la semana (del 1 al 7) devuelva el nombre de ese día como una cadena de caracteres. Por ejemplo, para el día 1 que devuelva ’Lunes’, para el 2, ’Martes’, y así sucesivamente. Para modelar este tipo de problemas contamos con una estructura especial, que llamaremos estructura alternativa múltiple, de la siguiente forma:

ALGORITMO nombreAlgoritmo() RETORNA ∅
    (* .... *)
    SEGUN expresionMultivaluada HACER 
        valor1: sentencias si expresionMultivaluada = valor1
        valor2: sentencias si expresionMultivaluada = valor2
        ...
        valorn: sentencias si expresionMultivaluada = valorn
    FIN SEGUN    
    ....
FIN ALGORITMO nombreAlgoritmo

ATENCION: En la estructura alternativa múltiple o tambien llamada estructura selectiva, la expresión no es booleana, sino de otro tipo (entero o caracter). Si la expresión fuera booleana deberiamos utilizar una estructura alternativa. En algunos lenguajes de programación el resultado de la expresión se restringe a los tipos entero y símbolo u otro tipo discreto, aunque en otros lenguajes se puede usar también texto.

Apliquemos la estructura de selectiva para resolver el problema de los días de la semana. La expresión a evaluar es el número entero día. Los valores posibles son los enteros del 1 al 7, y los valores no válidos (representado por la notación ∀o cuyo significado es ’para todo otro caso’) serán cualquier otro número. El diseño en pseudocódigo podría escribirse de la siguiente manera:

ALGORITMO diaSermana() RETORNA ∅
  (* Devuelve el nombre del dia de la semana de
  acuerdo a un numero entero 1 <= dia <= 7 *)
  TEXTO resultado
  ENTERO dia
  LEER(dia)
  SEGUN dia HACER 
    1: resultado ← "Lunes"
    2: resultado ← "Martes"
    3: resultado ← "Miercoles"
    4: resultado ← "Jueves"
    5: resultado ← "Viernes"
    6: resultado ← "Sabado"
    7: resultado ← "Domingo"
    ∀o: resultado ← "Error"
  FIN SEGUN
  ESCRIBIR(" corresponde a: ”+ resultado)
FIN ALGORITMO diaSemana ´

Por lo anterior, podemos resumir que la estructura selectiva evalúa una expresión multivaluada que puede tomar valores (o grupos de valores) distintos (\(e_1\),\(e_2\), … ,\(e_n\)).

Luego, según el valor que tome la expresión multivaluada, se realiza sólo una de las acciones posibles, o lo que es lo mismo, el flujo del algoritmo sigue un determinado camino entre los n posibles caminos. En la figura a continuación puede verse el diagrama de flujo para la situación de los días de la semana. La alternativa presenta 8 posibles caminos, del 1 al 7 son caminos válidos, pero si recibe un valor distinto va a devolver un texto Error.

El lenguaje Java tiene un constructor para implementar una estructura de este tipo. Es la sentencia switch que mostramos a continuación:

public class PrimerPrograma
{
public static void main( String[] args )
{
  // Declaración de variables   Scanner sc = new Scanner(System.in);
        String resultado;
        int dia;
        System.out.println("Ingrese un dia de semana 1-7");
        dia = sc.nextInt();
        switch (dia) {
            case 1: resultado = "Lunes"; break;
            case 2: resultado = "Martes"; break;
            case 3: resultado = "Miercoles"; break;
            case 4: resultado = "Jueves"; break;
            case 5: resultado = "Viernes"; break;
            case 6: resultado = "Sabado"; break;
            case 7: resultado = "Domingo"; break;
            default: resultado = "Error"; break;
        }
        System.out.println(dia + "corresponde a: "+ resultado);
    }
}

La forma general de switch es al siguiente:

  switch (expresiónMultivalor) {  ´
    case valor1: conjunto de sentencias; break;
    case valor2: conjunto de sentencias; break;
    case valor3: conjunto de sentencias; break;
    ....
    case valorn: conjunto de sentencias; break;
    default: conjunto de sentencias; break;
  }´

La sentencia switch evalúa la ExpresionMultivalor y ejecuta el ConjuntoDeSentencias que aparece junto a la cláusula case cuyo valor corresponda con ExpresionMultivalor. Cada sentencia case debe ser única y el valor que evalúa debe ser del mismo tipo que el devuelto por la ExpresionMultivalor de la sentencia switch.

Las sentencias break que aparecen tras cada ConjuntoDeSentencias provocan que el control salga del switch y continúe con la siguiente instrucción al switch. Las sentencias break son necesarias porque sin ellas se ejecutarían secuencialmente las sentencias case siguientes. Existen ciertas situaciones en las que se desea ejecutar secuencialmente algunas o todas las sentencias case, para lo que habrá que eliminar algunos break.

Finalmente, se puede usar la sentencia default para manejar los valores que no son explícitamente contemplados por alguna de las sentencias case. Su uso es altamente recomendado.

9. Videos de Clases Teóricas

• Primera clase del tema Estructura de control Alternativa, 20 de Abril de 2022: [https://youtu.be/n-PlrkvNr8E]
• Segunda Clase del tema Estructura de control Alternativa, 28 de Abril de 2022: [https://youtu.be/QNe4hk-9muw]