1. Introducción

Encontrar una representación adecuada para un problema frecuentemente resulta una gran ayuda para hallar la solución. Sin embargo, esto no siempre alcanza. Aún después de haber encontrado una o varias representaciones para el problema, puede resultarnos difícil avanzar. En ocasiones, es difícil encontrar una buena representación al menos decidir si la que hemos hallado es la adecuada, sin realizar algún trabajo previo. Veremos algunas estrategias que nos orientarán acerca de cómo encarar la búsqueda de una solución para un problema. Estas estrategias fueron presentadas en el libro de Polya.

Una estrategia. es un método general que puede aplicarse para hallar la solución de muchas clases de problemas. Una táctica. un método especial para hallar soluciones para problemas de una clase restringida.

Las estrategias que propondremos son de utilidad para problemas generales, en los que no se requiere un conocimiento específico. Por supuesto que no podremos abarcar problemas que requieran un conocimiento que no poseemos. Por ejemplo: no podemos decidir qué movida nos acercará a una configuración ganadora en un partido de ajedrez, si no sabemos jugar ajedrez.

Las estrategias que explicaremos nos permitirán mayor flexibilidad cognitiva Esta flexibilidad refiere a las funciones mentales para adoptar estrategias cambiantes o modificar el punto de vista y están especialmente implicadas en la resolución de problemas.

2. Inferencia

Hemos visto que la mayoría de los enunciados de problemas dados contenían o implicaban determinados hechos y de esos hechos podíamos deducir o inferir otros. El número de hechos que podemos inferir es usualmente grande y el arte consiste en seleccionar, de los hechos que tenemos disponibles, aquéllos que son relevantes para la solución.

En la primera versión de la solución del problema de las edades de Clariobaldo y Anabela, el no contar con una representación adecuada nos obligó a realizar una serie de inferencias. En cada paso fuimos deduciendo nuevos hechos. Cuando encontramos una representación equivalente en notación matemática, no fue necesario utilizar inferencias.

Ejemplo: Los caballeros y los escuderos. Una isla está habitada por caballeros que siempre dicen la verdad y por escuderos que mienten siempre. Se supone que todo habitante de la isla es o caballero o escudero.

Tres habitantes de la isla Richard I, Henry IV y Charles III, se encontraron en un jardín. Un extranjero le pregunta a Richard I: -¿Eres caballero o escudero?- . Richard I respondió tan confusamente que el extranjero no entendió. Entonces preguntó a Henry IV: -¿Qué dijo Richard I?- Henry IV respondió: -Richard I ha dicho que es escudero-. Pero entonces Charles III dijo: -No creas a Henry IV, ¡está mintiendo!-

¿Puede el extranjero saber qué son Richard I, Henry IV y Charles III?
En caso de que pueda, ¿qué son?

En este caso es posible hallar una solución para el problema manteniendo la notación verbal en la que está planteado.

Es imposible que un caballero o un escudero digan: - ‘Yo soy escudero’}, porque si esto lo dijera un caballero estaría mintiendo y si lo dijese un escudero estaría diciendo la verdad y, ni los caballeros mienten ni los escuderos dicen la verdad. Por lo tanto, Richard I nunca diría que es un escudero. De esto podemos deducir que Henry IV mintió cuando dijo que Richard I había dicho que él era escudero, por lo tanto Henry IV es escudero. Como Charles III dijo que Henry IV mentía, y efectivamente Henry IV mentía, esto nos está diciendo que Charles III es caballero.

Es imposible saber qué es Richard I, ya que ha dicho que era caballero pero no sabemos si está diciendo la verdad o miente y no hay manera de determinarlo.

Ejemplo 2: El edificio. Juan y José se encuentran frente al edificio en el que vive José y conversan:
José: Sí, me casé y tengo tres hijas.
Juan: ¡Qué bien! ¿Qué edad tienen?
José: El producto de sus edades es 36.
Juan: Hmm. Eso no me alcanza, dame otra pista.
José: La suma de sus edades es el número de mi edificio.
Juan: Ah, casi tengo la respuesta, pero aún necesito otra pista.
José: Muy bien. Ayer fue el cumpleaños de la mayor, que es pelirroja.
Juan: ¡Ya lo tengo!

Se desea encontrar una terna de edades que satisfagan las condiciones dadas.
El paso siguiente podría ser eliminar datos que resulten irrelevantes. En este caso, el hecho de que una de ellas sea pelirroja no parece relevante.
En general, es natural ir rescatando la información en el orden en que aparece en el enunciado.
Los primeros datos relevantes parecen ser que tiene TRES hijas y que el producto de sus EDADES es 36.
Así podemos formar todas las combinaciones de edades cuyo producto es 36 como muestra la siguiente Tabla \(\ref{tabla1}\).

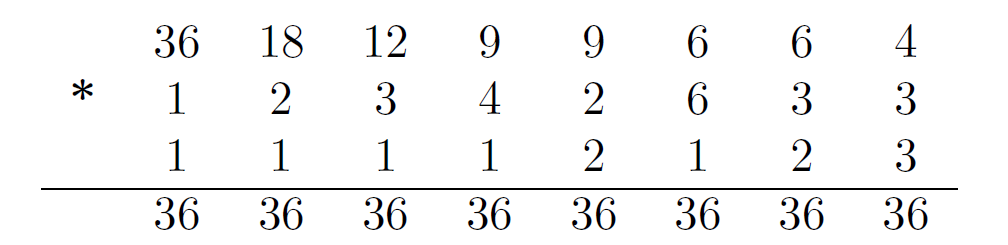
El siguiente dato es que el número del edificio en el que se encuentran es igual a la suma de las edades de las tres. Si sumamos las edades obtenemos la Tabla \(\ref{tabla2}\).:

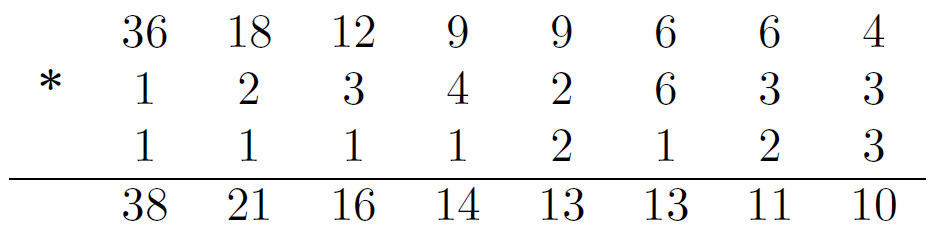
En este punto podemos quedar desorientados y no saber cómo seguir. ¿Cuál es el obstáculo? Nosotros no conocemos el número del edificio, pero Juan sí. ¿Qué podemos inferir de este hecho? Si el número del edificio fuera 38, 21, 16, 14, 11 o 10, Juan hubiera tenido la respuesta. Sin embargo, necesitó una pista más, ¿por qué? Como la dirección era 13, había dos combinaciones posibles. En ambas, dos de las hijas son mellizas, en el primero, las menores; en el segundo, las mayores. La última pista indicaba que una sola, la mayor, había cumplido años. Por lo tanto, la única configuración válida era 9, 2, 2.

Ejercicio 3 Uno de perlas: Se tienen 24 perlas y se sabe que una es más pesada que el resto y no puede distinguirse por su aspecto. Además, se cuenta con una balanza con dos platillos. Identifique la perla más pesada con no más de tres pesadas. ¿Es posible? ¿Es éste el mínimo número de pesadas necesarias para encontrar la perla defectuosa?

Tenemos una balanza con 2 platillos, y en cada uno de ellos podríamos poner la mitad de las perlas. Dependiendo de hacia dónde se incline la balanza, podremos detectar en que grupo de 12 se encuentra la perla defectuosa. Luego sacamos las perlas de la balanza y, al grupo más pesado lo dividimos nuevamente en dos procediendo de la misma manera.

En este caso, veamos que una buena representación puede ser la siguiente:

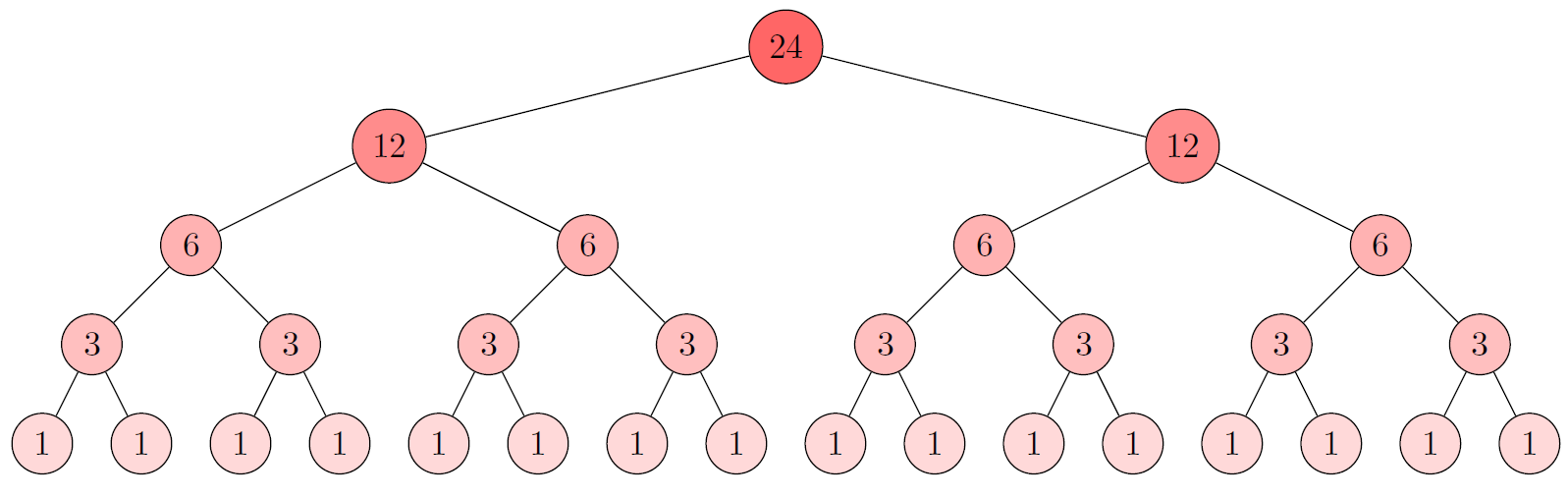
Cada nivel (con excepción del nivel raíz) representa una pesada y tenemos representadas todas las posibles pesadas que pueden efectuarse. Luego de tres operaciones de pesadas aún tenemos 3 (o cuanto mínimo dos) perlas, una de las cuales puede ser la más pesada, pero no sabemos cuál. Por lo tanto, no es suficiente dividir cada vez en dos al conjunto conteniendo la perla más pesada para cumplir con la restricción de tres pesadas.

¿Qué ocurre si dividimos la cantidad de perlas a pesar? En este caso podríamos pensar en dividir en 3 el conjunto de las 24 perlas, pesando dos de los grupos y dejando el tercer grupo sin pesar. En este caso, si los platillos de la balanza se mantienen en equilibrio, el grupo donde se encuentra la perla no es ninguno de los 2 que están pesándose. Tomamos entonces el grupo donde se encuentra la perla más pesada, que sí lo podemos determinar y repetimos el procedimiento. El espacio de soluciones puede plantearse nuevamente como un árbol y lo visualizamos del siguiente modo:

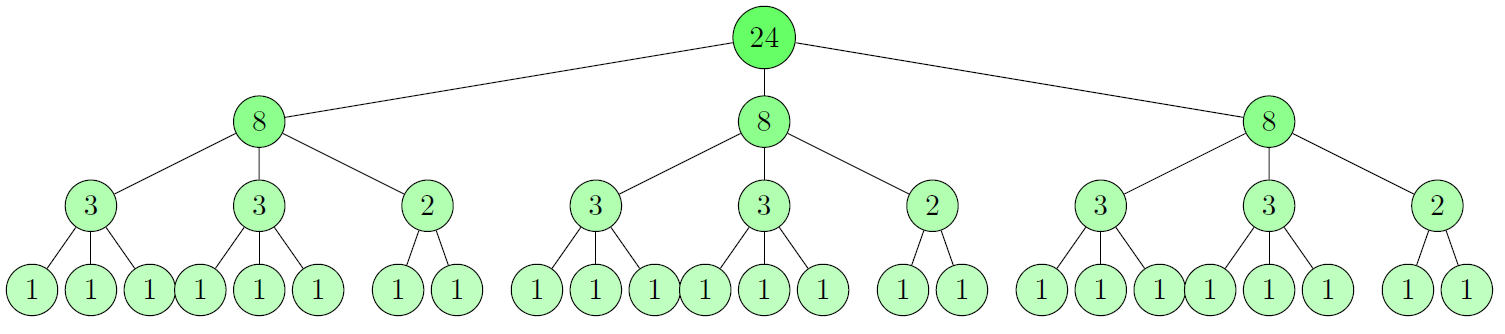
Vemos que, en este caso, sí es posible determinar cuál es la perla más pesada utilizando la balanza sólo tres veces.

3. Afinidades entre Problemas

La complejidad para hallar la solución de un problema depende en gran medida de cuán original nos resulte.

Comúnmente una persona no se enfrenta a problemas aislados, totalmente independientes entre sí. Encontrar la similitud de un problema con algún otro resulta por lo general muy útil.

Si encontramos un problema similar para el cual ya conocemos el modo de llegar a su solución, podemos aplicar el mismo modo de hallar la solución en el problema original.

Un inconveniente que se presenta al tratar de hallar la solución de un nuevo problema de acuerdo a problemas solucionados anteriormente, es caer víctima de Einstellung . Mediante este vocablo designamos al proceso por el cual siempre se trata de aplicar el mismo procedimiento, llevado por la costumbre o la inercia. Podemos caer en una situación tal donde el método tradicional sirve, pero existe una solución más rápida o eficiente. Esta cadencia impide ver la nueva situación.

Ejemplo 4 Capacidades. Supongamos que contamos con tres recipientes y una canilla de la cual podemos sacar toda el agua que queramos. El recipiente A puede contener 21 decilitros de agua, el B puede almacenar 127 decilitros y el C sólo 3 decilitros. Sólo cuenta con estos recipientes y debe medir 100 decilitros. ¿Cómo lo hace?

La solución a esto puede ser la siguiente: llenar el recipiente B con agua, luego llenar el A con agua extraída del B y luego llenar el recipiente C dos veces extrayendo agua también del recipiente B. Entonces tendremos 100 decilitros en el recipiente B.

Supongamos ahora que en el recipiente A tenemos 13 decilitros, B contiene 163 decilitros y C, 25 decilitros. Si debemos medir 100 decilitros, ¿qué debemos hacer? Es claro que lo mismo.

¿Qué hacemos ahora si el recipiente A contiene 23 decilitros, el B 49 y el C 3, y debemos medir 20 decilitros? Podemos hacer lo mismo que hemos hecho hasta el momento. Esto es fácil verlo.

Pero, si analizamos claramente este último caso en particular, vemos que hay una manera mucho más fácil de hacerlo, ya que sólo basta llenar el recipiente A y extraer el agua de A con el recipiente C sólo una vez. Hemos sido víctimas del Einstellung.

4. Semejanza y Analogía

En el siglo XVI el fundamento de toda interpretación era la semejanza. La semejanza jugó un papel importante en la Botánica, la Antropología, entre otras disciplinas. La naturaleza era pensada como un juego de signos y semejanzas que se entrecruzaban infinitamente Foucault (1970). El sistema de interpretaciones de la vida misma en aquel siglo estaba organizado bajo cinco nociones: la conveniencia del alma al cuerpo, del reino vegetal al animal; la identidad de accidentes en sustancias distintas (simpatía); el paralelismo de atributos en seres distintos (* emulatio); la identidad de relaciones en dos entre sustancias distintas (analogía*); etc.

Si bien hemos evolucionado en la explicación de un montón de fenómenos en las distintas disciplinas, la semejanza y la analogía siguen constituyendo hoy poderosas herramientas de razonamiento y estrategias para la resolución de problemas. De hecho, a medida que se va adquiriendo cierta experiencia en la resolución de problemas, es frecuente, ante una nueva situación, encontrar semejanzas con otras resueltas con anterioridad. Por lo general, no resolvemos un problema desde cero. Esto nos proporciona confianza.

Ejercicio 5: El Juego del 15. Dos jugadores juegan sobre una tabla con nueve casillas marcadas del 1 al 9. Por turnos, cada uno coloca una ficha sobre una casilla libre. Gana el primero que sume 15 con tres fichas distintas.

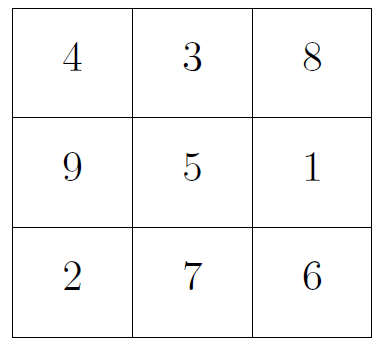
Al experimentar con este juego nos familiarizamos con las combinaciones de números que permiten ganar partida. Si hemos trabajado con cuadrados mágicos, reconoceremos en esas combinaciones las filas, columnas y diagonales del cuadrado mágico más famoso, el de suma 15. La representación del desarrollo del juego con las fichas sobre dicho cuadrado mágico es semejante al juego del “tres en raya”. Entonces, la estrategia está clara: convertir el juego inicial en un “tres en raya” ó Tic Tac Toe, sin que el adversario lo advierta.

La analogía es un tipo de similitud Polya (n.d.). Podríamos decir que es una similitud en un nivel más conceptual y preciso. Los objetos similares coinciden entre ellos en algunos aspectos. Si intentamos reducir el aspecto en el cual coinciden bajo conceptos muy precisos, veremos estos objetos similares como análogos.

La comparación entre una bomba y el corazón es una analogía válida. Son entidades dispares, pero comparten cualidades importantes: son aparatos mecánicos, poseen válvulas, pueden subir y bajar presiones y tienen la capacidad para mover fluidos. Además, el corazón y la bomba exhiben estas cualidades en formas distintas y en diferentes contextos.

Cuando se discute sobre una ciudad superpoblada, comparándola con otra, no ofrecemos una analogía, sino una comparación. Pero si comparamos una ciudad poblada con una colonia de hormigas, estamos poniendo en marcha una analogía. Las dos ciudades no son análogas pero sí lo son la ciudad y la colonia. Un barco tripulado por oficiales cruzando un mar tormentoso es una analogía común para un estado político que pasa por trances adversos. Los políticos suelen ser muy hábiles para definir metáforas de este tipo.

Como todas las metáforas, la analogía puede servir para propósitos retóricos. Una analogía tiene además una función descriptiva al permitir dar un símil vívido y conocido para que un concepto, demasiado abstracto o alejado de la experiencia ordinaria, pueda ser claramente entendido.

Objetos semejantes concuerdan unos con otros en algunos aspectos mientras que objetos análogos concuerdan en ciertas relaciones entre sus elementos respectivos Polya (n.d.).

Un paralelogramo rectangular es análogo a un paralelepípedo rectangular. De hecho, las relaciones entre los lados del paralelogramo son parecidas a las que existen entre las caras del paralelepípedo. Así expresamos ciertas relaciones comunes a los dos sistemas de objetos comparados: los lados del paralelogramo y las caras del paralelepípedo.

En el plano, dos líneas rectas no pueden constituir una figura finita, pero 3 pueden formar un triángulo.

En el espacio, tres superficies no determinan un cuerpo finito pero cuatro constituyen un tetraedro .

La relación del triángulo al plano es análoga a la establecida con el tetraedro al espacio, en cuanto a que ambos están limitados por el número mínimo de elementos.

¿Podemos considerar análogos al triángulo y a la pirámide?

Sí. Los podemos considerar análogos. Por un lado, tenemos un segmento de recta y por otro, un polígono. Si conectamos dos puntos del segmento de recta con un punto exterior al mismo, obtenemos un triángulo. Si conectamos todos los puntos del polígono con un punto exterior a la superficie del polígono, obtenemos una pirámide.

Debemos tener cuidado al establecer analogías ya que si no ha sido bien aclarada puede ser ambigua. Así, comparando la geometría plana y la sólida encontramos que un triángulo en el plano es análogo a un tetraedro en el espacio y también a una pirámide. Ambas analogías son válidas y cada una valiosa en su aspecto.

5. Particularización

Particularizar consiste en pasar de un conjunto de objetos dado a un conjunto más pequeño o incluso de un solo objeto, contenido en el conjunto dado, es decir, pasar de la consideración de una serie determinada de objetos a la de una serie más pequeña contenida en la primera. También se llama especialización.

Por ejemplo, especializamos cuando pasamos de la consideración de polígonos a la de polígonos regulares y especializamos aún más cuando pasamos de polígonos regulares con n lados a triángulos.

Estos dos pasos subsecuentes fueron efectuados de dos maneras típicamente diferentes. En el primero, de polígonos a polígonos regulares, introdujimos una restricción, esto es, que todos los lados y los ángulos del polígono son iguales. En el segundo paso, sustituimos un objeto variable por uno determinado: pusimos 3 en lugar de n.

Una sola excepción basta para refutar irrevocablemente lo que pretende ser una regla o una afirmación de carácter general. El método más corriente y con frecuencia el mejor para refutar tal proposición consiste precisamente en encontrar un objeto que no encuadre con ella; ciertos autores llaman a dicho objeto contra-ejemplo.

La proposición que por hipótesis es general, concierne a un cierto conjunto de objetos; para refutarla particularizamos eligiendo, en dicho conjunto, un objeto que no se cuadre a ella.

Podemos examinar, en principio, cualquier caso particular sencillo, es decir, un objeto, elegido al azar, en el cual podamos facilmente verificar la proposición. Si la experiencia muestra que el caso no encuadra en la proposiciòn general, esa se dá por refutada, quedando terminada nuestra labor.

Los casos extremos son particularmente instructivos.

Ejercicio: Refutar las siguiente Regla:

Todos los mamíferos son terrestres

Si la afirmación general es aplicable a todos los mamíferos, debe aplicarse igualmente a un mamífero tan raro como la ballena. Los casos extremos suelen ser olvidados por los inventores de generalidades.

Luego, es claro que el caso:

la ballena es un mamífero, que es acuático, es un contraejemplo a la regla.

Encontrar un contraejemplo, exige el empleo de la estrategia de especialización y la búsqueda de contraejemplos ha sido la base del falsacionismo. El falsacionismo, refutacionismo o principio de falsabilidad es una corriente epistemológica fundada por el filósofo austríaco Karl Popper . Para Popper, contrastar una teoría significa intentar refutarla mediante un contraejemplo.

Ejercicio 7: Refutar las siguientes afirmaciones:

6. Generalización

La generalización consiste en pasar del examen de un objeto al examen de un conjunto de objetos, entre los cuales figura el primero, o pasar de un conjunto limitado de objetos a un conjunto más extenso que incluya al conjunto limitado.

Dada la suma \(1 + 8 + 27 + 64 = 100\), podemos observar que puede expresarse bajo la forma curiosa: \(1^3 + 2^3 + 3^3+ 4^3 = 10^2\). Es natural entonces plantearse la pregunta: ¿sucede con frecuencia que la suma de cubos sucesivos tales como \(1^3 + 2^3 + 3^3 + ... + n^3\) es un cuadrado? Haciendo tal pregunta estamos intentando hacer una generalización.

Muchos resultados se han obtenido en Matemática, Física y Ciencias Naturales, gracias a generalizaciones de este tipo. Debemos tener sumo cuidado cuando tratamos de realizar generalizaciones, es decir, cuando tratamos de extender el comportamiento de un objeto a la clase de objetos a la cual pertenece. Es necesario observar que las mismas propiedades se siguen cumpliendo y es conveniente una prueba formal del resultado obtenido.

Una serie de ejemplos típicos de generalización surge al buscar fórmulas matemáticas. Mediante una fórmula se trata de estandarizar el comportamiento de una situación, tal que, al enfrentarnos a un caso particular de dicha situación, sepamos cómo hallar la solución.

Los problemas de particularización y generalización muchas veces pueden verse como dos caras de la misma moneda (he aquí una analogía). De varios casos particulares tratamos de deducir un comportamiento general, representado mediante una fórmula. Cuando estamos en presencia de un caso concreto, aplicamos la fórmula y tenemos resuelto el problema.

En el caso de la sumatoria anterior vemos que, probado el resultado general: \(1^3 + 2^3 + 3^3 + ... + n^3 = (1+2+3 + ... + n)^2\), podemos aplicarlo a : \(1^3 + 2^3 + 3^3 + 4^3 + 5^3 = 15^2\).

También hemos usado este método de generalización y particularización en la escuela primaria. Los problemas típicos, en aquel entonces, eran del tipo: “Don Jorge tiene un campo de forma trapezoidal y desea rodearlo con doble vuelta de alambre; las medidas del campo son …. ¿Cuántos metros de alambre necesita?

El hecho de usar fórmulas es reconocer su utilidad en el momento adecuado. En el caso anterior, usar la fórmula para calcular el perímetro de un trapecio y luego multiplicarlo por dos, parece una idea obvia, aunque en realidad, deberíamos preguntarnos si la idea es realmente obvia o estamos muy acostumbrados a este tipo de problemas y por lo tanto la solución surge por asociación a problemas ya resueltos.

Antes de realizar el ejercicio tengamos en cuenta lo siguiente: multiplicar dos números es igual a crear una red cuyos lados representan estos valores. Por ejemplo: 2*3 se puede visualizar como la siguiente red de dos nodos de alto por tres nodos de largo.

Ahora comencemos con el ejercicio :

Generalización: ¿Cómo podemos generalizar cuál es el valor de la suma de los n primeros números naturales?,

es decir \(1+2+3+ ... +n =\) ?.

Analicemos algunos de los primeros casos, por ej.: cuando n es igual a 2, 3, 4, etc.

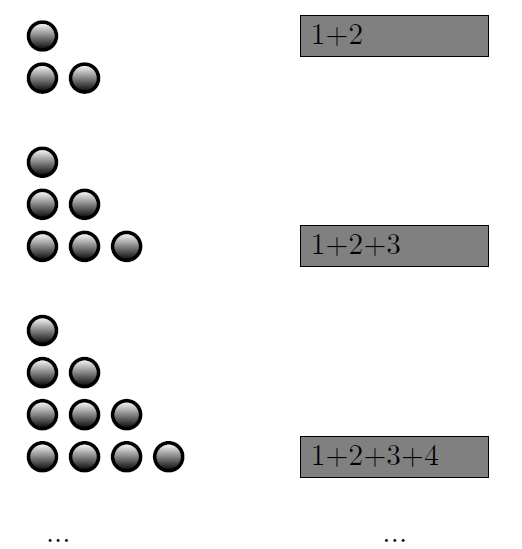
Encontrar el resultado para los primeros casos no es complejo, pero el desafio está en encontrar una expresión genérica para el resultado en función del valor de n.

Si no nos hemos dado cuenta aún, que es lo mas probable, tal vez la siguiente figura nos ayudará. Tener presente al ver la figura que los círculos grises claros representan el resultado a generalizar en función de un conjunto.

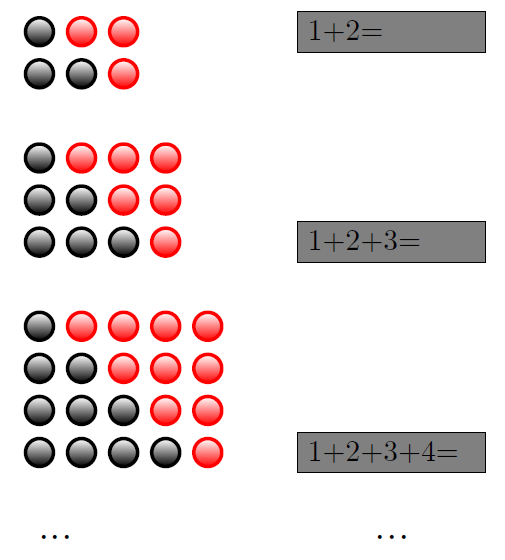Estos mecanismos de generalización y particularización deben emplearse con extrema prudencia. Si sólo se tiene en cuenta algunos ejemplos, esto no nos permite deducir el comportamiento global. Para que un resultado de una generalización sea aceptable se requiere una prueba formal.

La generalización es muy útil al desarrollar algoritmos y programas. Debemos estar seguro que nuestro algoritmo es válido para un conjunto de instancias. Mas adelante veremos también que las estructuras de control repetitivas que definiremos permiten modelar la repetición de un conjunto de casos. En estos casos debemos constantemente tener en cuenta las estrategias de particularización y generalización Reynoso et al. (2013).

Supongamos que un problema dice: “Tres obreros tardan 8 horas en hacer un pozo de 2 metros de diámetro y 15 de profundidad. ¿Cuánto tardarán 1000 hombres en hacer el mismo trabajo? ¿Podríamos suponer la aplicación de una relación lineal? NO. Su aplicación es totalmente fatua en este caso.

%Una señora tarda 9 meses en tener un bebé. ¿Cuánto tardarán 2 señoras?

¡Debemos tener sumo cuidado con la generalización!

7. Versión pdf

Una versión pdf de este apunte lo podes encontrar en: link

8. Videos clases anteriores

9. Referencias

Foucault, M. 1970. Nietzsche, Freud, Marx. Editorial Anagrama. Ensayo Filosofía.
Polya, G. n.d. How to Solve It, a New Aspect of Mathematical Method. Princeton University Press. Princeton, New Jersey.
Reynoso, L., J. Rodriguez, L. Sanchez, and M. Alvarez. 2013. “Technicians and Their Learning Styles Preferences and Cognitive Processes of Formal Inferences.” Proc. IEEE 12th International Conference on Cognitive Informatics & Cognitive Computing (ICCI*CC 2013), 51–60.