Apunte: Problemas
RPA- Dr.Luis Reynoso
01 abril, 2023
1. Introducción
Ver video Introducción: [https://youtu.be/AREkE26OsKM]
Aprender a afrontar y resolver problemas es un
importante reto en nuestra vida cotidiana. De otra forma los problemas
podrían agobiarnos. Enfrentamos problemas simples o complejos, por
ejemplo: ¿cómo llegar hasta lo de un amigo que deseamos visitar? ¿cómo
ganar una partida de ajedrez? ¿qué hacer para ganar más dinero? ¿cómo
ser feliz?. En todo problema debemos buscar de forma consciente
una acción apropiada para lograr un objetivo claramente
concebido, pero no alcanzable en forma inmediata
[Polya, 1965]. Un problema puede considerarse una discrepancia
entre un estado actual o inicial y un estado deseado o final. Y,
para pasar de un estado a otro realizamos determinadas tareas que
denominamos acciones. Hallar una solución del problema puede pensarse
como un proceso de selección. Cuando el problema es escribir una carta,
la solución consistirá en una combinación de palabras que expresen lo
que queremos decir. Si el problema es ejecutar una operación aritmética,
el resultado será un número. En cualquier caso, estamos seleccionando
una respuesta adecuada. En nuestra materia de Resolución de Problemas y
Algoritmos, como bien lo indica el nombre resolveremos problemas. El
desarrollo de la misma se centrará en actividades teórico-prácticas, en
las cuales en forma reiterada abordaremos problemas de complejidad
incremental. Este documento detalla varios aspectos relacionados con el
concepto de problemas. La sección 2 describe tres categorías de
problemas que nos permitirán utilizar términos y vocabulario en el tema.
La sección 3 introduce un método muy simple para resolver problemas cuyo
autor es George Polya [Polya, 1973]. La sección 4 desarrolla el tema de
representaciones utilizadas al resolver problemas. Estas
representaciones nos ayudarán a esquematizar los objetos y relaciones
del problema.
2. Algunas Categorías de Problemas
Ver video Categorías Iniciales de Problemas: [https://youtu.be/KV4uMascLyk]
2.1. Según su Formulación
Según como haya sido formulado un problema, podemos distinguir dos categorías: En la primera, el planteo del problema viene dado como una descripción de los estados inicial y final. Hallar la solución consiste en seleccionar una sucesión de estados intermedios de acuerdo a ciertas reglas. Este tipo de problemas pueden ser considerados de síntesis ya que la incógnita son los pasos intermedios entre dos estados dados.
Incógnita: Mat. Cantidad desconocida que es preciso determinar en una ecuación o en un problema para resolverlos.
Ejemplo 2.1 Encontrar una secuencia de palabras del idioma castellano que permitan pasar de
LIS a SOL con palabras intermedias. En cada paso sólo es posible cambiar una sola letra de la
palabra del paso anterior. Para este ejemplo el estado inicial es LIS y el estado final es SOL.
Una solución válida consistirá en 2 palabras castellanas que permitan pasar de una a otra de
acuerdo a las restricciones dadas LIS LOS SOS SOLLa segunda categoría de problemas incluye a todos aquellos planteos en los que se presenta un estado inicial y un conjunto de restricciones que debería satisfacer el estado final. Estos problemas pueden ser considerados como de análisis ya que la incógnita es ahora el estado final.
Ejemplo 2.2 ¿Qué porcentaje de 120 representa 30?
En este último ejercicio el estado inicial esta representado por el hecho de conocer que 120
representa el 100 % de dicha cantidad. Deseamos conocer que porcentaje representa una parte de
esta cantidad (30 de 120). El estado final consiste en hallar el porcentaje que representa 30 de 120.2.2. Según su Tipo de Solución
Según otro punto de vista, podemos distinguir aquellos problemas cuya solución es subjetiva de aquellos que tienen una solución objetiva.
Si nuestro problema es comprar un auto o decorar una casa, la solución puede ser muy subjetiva. El mismo problema, según diferentes sistemas de valores y criterios, puede dar lugar a soluciones muy dispares y probablemente contrapuestas. Normalmente el planteo de estos problemas viene dado en forma más o menos vaga y es muy difícil describir todos los factores que intervienen en la selección de la solución.
Existen problemas para los cuales es posible hallar una solución que no dependa de elementos subjetivos. El planteo contiene entonces un conjunto de condiciones o restricciones que permiten decidir si una respuesta constituye una solución o no para el problema. Para los problemas de los ejemplos 2.1 y 2.2 es posible hallar soluciones objetivas, que no dependen de ninguna escala de valoración. Nos ocuparemos únicamente de este último tipo de problemas.
2.3. Según Cantidad de Soluciones
Desde el punto de vista del número de soluciones, los problemas se pueden clasificar en:
En el campo de la Matemática, por ejemplo:
- x 2 + 1 = 0, no tiene solución en el campo de los números reales.
- x + 4 = 7 tiene una única solución.
- x + y = 5 tiene varias soluciones en el campo de los números naturales (N).
- x + y = 5 tiene infinitas soluciones en el campo de los números reales (R).
3. El Método de Polya
Ver video de los pasos de Polya: [https://youtu.be/O7hWDy_unr0]
George Polya [Polya, 1973] proporcionó heurísticas generales para resolver problemas de todo tipo, no sólo matemáticos. El libro “How to solve it”, cuya primera versión fue en 1945, incluye consejos para enseñar Matemática a los estudiantes y una mini-enciclopedia de términos heurísticos. Ha sido traducido a muchos idiomas y vendido más de un millón de copias. Según Wikipedia, el físico ruso Zhores I. Alfyorov (Premio Nobel de Física de 2000) lo alabó, diciendo que estaba encantado con el famoso libro de Polya. El método de 4 pasos que propone Polya se resume en la Figura 5. De acuerdo a Polya [Polya, 1973] ’primero, tenemos que comprender el problema, es decir, ver claramente lo que se pide. Segundo, tenemos que captar las relaciones que existen entre los diversos elementos, ver lo que liga a la incógnita con lo datos a fin de encontrar una idea de la solución y poder trazar un plan. Tercero, poner en ejecución el plan. Cuarto, volver atrás una vez encontrada la solución, revisarla y discutirla’.
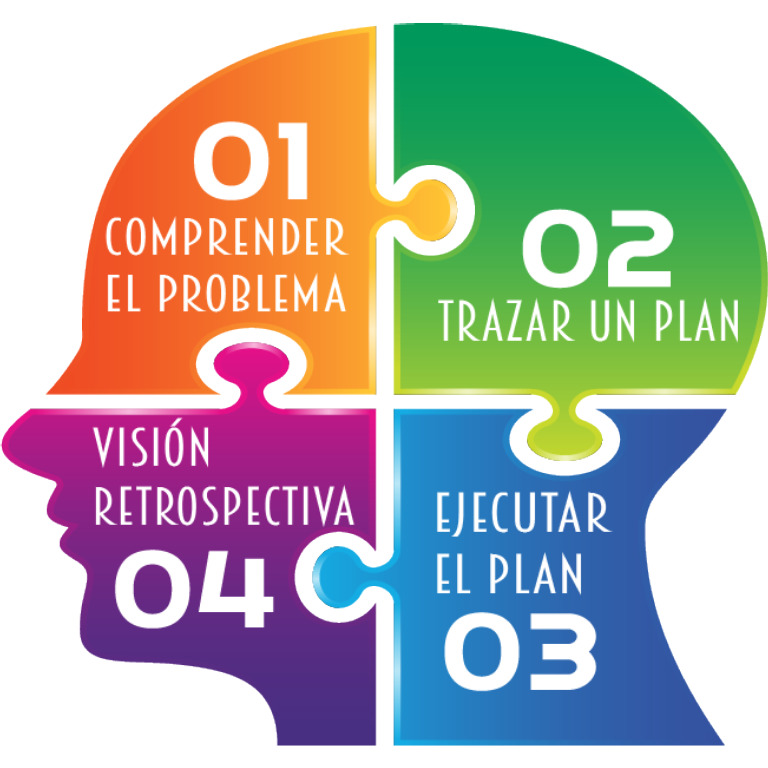
El método de Polya incluye una lista de preguntas para cada paso, relacionadas con la operaciones intelectuales particularmente útiles para la solución de problemas. Ellas tienen un sentido y ayudan a esclarecer el problema. Sugieren un camino a seguir que llevará al alumno con frecuencia al éxito. Ayudan a hacer explícito un comportamiento, un razonamiento, etc. Si una persona “emplea la misma pregunta varias veces con buen resultado, sin duda se fijará en ella y a ella recurrirá cuando se encuentre en un caso similar” [Polya, 1973]. Es importante realizarse las preguntas indicadas en el momento adecuado y efectuar con toda naturalidad la operación intelectual correspondiente. El resolver problemas es una habilidad práctica y es imprescindible desarrollar una aptitud para resolver problemas [Reynoso et al., 2012]. Es importante a la hora de resolver problemas interesarnos en ellos y prestar mucha atención de posibles ocasiones en las cuales veamos como otros resuelven problemas para poder imitarlos y poner en práctica una solución similar.
3.1. Comprender el problema
El paso de Comprender el problema incluye entender claramente cuál es la incógnita, cuáles son los datos y cuál es la condición. Se recomienda formularse preguntas tales como: —¿Entiendo todo lo que dice? —¿Puedo replantearme el problema con mis propias palabras? —¿Distingo cuáles son los datos? —¿Me doy una idea a qué quiero llegar? —¿Hay suficiente información? —¿Hay información extraña? —¿Este problema es similar a algún otro que he resuelto antes?
3.2. Trazar el plan
El paso de trazar un plan propone utilizar alguna/s estrategia/s2 . Tenemos un plan cuando sabemos a “groso modo” qué cálculos, qué razonamientos o construcciones habremos de efectuar para determinar la incógnita [Polya, 1973]. Las estrategias pueden ser:
- Ensayo y error (conjeturar y probar la conjetura
- Usar una variable.
- Buscar un patrón
- Hacer una lista.
- Resolver un problema similar más simple.
- Hacer una figura.
- Hacer un diagrama.
- Usar las propiedades de los números.
- Resolver un problema equivalente.
- Trabajar hacia atrás.
- Usar casos.
- Resolver una ecuación.
- Buscar una fórmula.
- Usar un modelo.
- Identificar submetas, etc.
3.3. Ejecutar el plan
El paso de Ejecutar el plan consiste en implementar la o las estrategias seleccionadas en el punto anterior hasta solucionar completamente el problema o hasta que la misma acción sugiera tomar un nuevo curso.
3.4. Vision Retrospectiva
El paso de Visión retrospectiva involucra planterse las siguientes preguntas:
*¿La solución es correcta?
*¿La respuesta satisface lo establecido en el problema?
*¿Hay alguna otra solución más sencilla al problema?
*¿Puedo probar el resultado obtenido?
Comúnmente, los problemas se enuncian en palabras, ya sea oralmente o en forma escrita. Así, para resolver un problema, uno traslada las palabras a una forma equivalente del problema en la que usa símbolos (por ej. matemáticos), resuelve esta forma equivalente y luego interpreta la respuesta. A continuación, veremos distintas construcciones o representaciones que nos permitirán modelar el problema
Puedes probar tus conocimientos respondiendo las siguientes preguntas:
4. Plantilla para Resolver Problemas
Utilizaremos la siguiente plantilla al resolver cada enunciado del práctico ([http://opendata.fi.uncoma.edu.ar/Plantilla.docx]). Esta plantilla tiene un objetivo: y es, ir internalizando algunos pasos que nos permitirán arribar a una solución. Estos pasos se pueden subsumir en el método de resolución de problemas de Polya, sin embargo nos permiten estructurar y clarificar nuestra solución.

La plantilla tiene este formato:
| Componente | Detalle |
|---|---|
| Identificador/Ejercicio: | |
| Objetivo del Problema | |
| Datos Relevantes | < Incluímos la información conocida y que detectamos que sirve para resolver el problema> |
| Representación. | <Detallamos la representación: fórmulas, gráficos, relaciones existentes entre los datos relevantes> |
| Secuencia de Pasos | |
| Resultado | <Expresamos claramente el resultado obtenido, el cual se corresponde con el objetivo> |
| Verificación |
Describimos un poco más cada uno de sus componentes y los ponemos en relación con Polya:
| Componente | Detalle |
|---|---|
| —Identificador | En el indicamos el número del ejercicio y el práctico al cual corresponde. |
| —Objetivo: | Indicamos cual es el objetivo del problema, al cual deseamos llegar. El objetivo debe estar claro y está relacionado con la comprensión del problema. |
| —Datos Relevantes: | En este item incluímos todos aquellos datos relevantes del enunciado que estan en relación con el objetivo perseguido. No incluímos los datos irrelevantes o superfluos. |
| —Representación: | Incluimos en este ítem la relaciones entre los objetos del problema. Los datos relevantes estarán seguramente relacionados entre sí. Podemos enunciar alguna forma de representación como un diagrama, fórmula, etc. Este ítem está en relación con el paso de Trazar un plan de Polya. |
| —Pasos: | Incluimos en este item el desarrollo de pasos, que permiten mostrar cómo a partir de los datos principales del enunciado es posible arribar a un resultado. Por ejemplo, al mostrar el desarrollo de una ecuación. En cada paso del desarrollo debemos poder justificar las razones del paso. No debemos omitir ningun paso intermedio. |
| —Resultado: | Expresamos el resultado, o los resultados. El resultado esta en relación con el objetivo perseguido. Debemos expresarlo claramente, y expresar la unidad de medida del mismo. |
| —Verificación: | Expresamos una verificación del resultado. Realizamos una prueba de que el resultado es correcto de acuerdo a los datos proporcionados en el enunciado. Este paso está en relación con el paso de revisión retrospectiva del método de Polya. |
Video sobre Plantilla para Resolver Problemas: [https://youtu.be/6SyFuWZdLTs]
5. Representaciones
Para hallar soluciones a problemas se requiere habilidad, conocimiento y experiencia. Un problema puede ser simple o complejo según quien tenga que hallar su solución. Tal vez lo que es un problema para una persona no lo sea para otra, ya que las personas tenemos distintas capacidades para hallar soluciones a diferentes clases de problemas.
Aunque a veces es posible hallar la solución de un problema aparentemente difícil de una forma puramente intuitiva ya que podemos tener raptos de inspiración, en general, resulta conveniente tener presente que estrategias y tácticas nos pueden orientar en la búsqueda de soluciones de problemas. Estas tácticas y estrategias no necesariamente nos conducirán a la solución, pero es probable que nos ayuden en menor o mayor medida. La búsqueda de la solución de un problema es una tarea difícil de sistematizar. Cada problema puede presentarse en forma aparentemente aislada y frecuentemente no sabemos cómo encararlo. Sin embargo, existen algunas pautas útiles que, de ser seguidas, pueden ayudarnos para enfrentar el problema:
- Establecer el problema en forma clara y entenderlo completamente.
- Clarificar cualquier ambig¨uedad que presente el problema.
- Definir exactamente qué se quiere hacer.
- Especificar con precisión todas las restricciones o condiciones que debe satisfacer la solución.
- Identificar claramente la información disponible.
- Explicitar toda información implícita en el planteo que pueda resultar útil.
- Encontrar una representación adecuada para esta información.
- Retomar el enunciado original ante un callejón sin salida.
- Verificar la solución encontrada.
Estas pautas, que no son más que la sintesis de los cuatro pasos indicados por Polya no deben seguirse necesariamente en el orden antes expuesto; muchas tareas se repiten y a menudo se relee el enunciado con mayor detenimiento, focalizando la atención en algún aspecto que tal vez resultó inadvertido en un primer momento. Estas pautas van a ser imprescindibles cuando intentemos construir un programa (o software) a partir de un planteo o a partir de las necesidades expresadas por un usuario. Es frecuente que cuando deseamos hallar la solución del problema impongamos más restricciones a la incógnita que las implicadas en el enunciado. Por eso, en esto debemos ser cuidadosos, no hacer más complejo el problema de lo que es, y limitarnos a resolver el problema esencial.
Ejemplo 5.1 Lápices: Supongamos que tenemos seis lápices de igual longitud y deseamos formar cuatro triángulos equiláteros de igual tama˜no, sin que se crucen los lápices. Intente hallar la solución... (y luego siga leyendo).
La mayor parte de quienes se enfrentan a este problema han intentado formar figuras sobre una
mesa o en el suelo, restringiendo el problema al plano. Probablemente esta restricción se deba a la
asociación natural entre un triángulo y el plano. Intente ahora una solución en el espacio.
El enunciado anterior no establece ningún tipo de pauta para encontrar la solución; es más, se
aprovecha de la idea preestablecida de que la mesa es un plano, en el que se acomodaran los lápices
para formar los triángulos, pero el espacio es un conjunto infinito de planos.
En otras ocasiones, el enunciado impone, en forma más o menos explícita y precisa,
pautas para hallar la solución. En este caso, por ejemplo, podría haber dicho: no se restrinja
al plano.Existen algunos otros pasos que siempre que sea posible es importante aplicar. Por ejemplo, eliminar toda aquella información redundante o irrelevante. Sin embargo, es muy difícil decidir desde el principio qué datos podemos descartar pues no van a ayudarnos a hallar una solución.
Si bien la búsqueda de soluciones para problemas es una tarea creativa, en donde la imaginación y la intuición juegan roles importantes (también la experiencia), no debemos perder de vista que la aplicación de técnicas de re- solución de problemas es central en este tipo de tareas. Gracias a las técnicas no es necesario pensar individualmente cada instancia de solución desde cero. En cambio, podemos aplicar métodos ya desarrollados o exitosos a nuevas instancias de problemas. Un problema se presenta, en general, bajo la forma de un enunciado. No consideraremos el caso de enunciados incompletos, ambiguos o contradictorios porque en estos casos, el problema no está bien especificado y deberíamos comenzar por encontrar un planteo adecuado.
La principal dificultad para hallar la solución de un problema no es la falta de información, sino la incapacidad para utilizar convenientemente la información provista. Aún cuando un enunciado contenga información suficiente para hallar la solución del problema, es probable que haya información irrelevante, redundante o implícita. La capacidad de la mente para manipular información es muy limitada. La capacidad de la memoria de corto plazo fue estudiada por Miller [Miller, 1956] y Broadbent [Broadbent, 1975]. Miller encontró que el número máximo de conceptos que es posible retener en la memoria de corto plazo es 7 +/- 2. Por otro lado una persona retiene menos conceptos a la vez si no hay relación entre ellos, esto fue estudiado por Gopal [Gopal, 1991]. De aquí la importancia de establecer relaciones entre los datos del problema, realizar un tratamiento con ellos de tal manera de conceptualizarlos de una forma más adecuada y resumida.
Ejemplo 5.3 Observe la siguiente secuencia de dígitos durante 10 segundos:
3 0 7 1 5 9 4 6 2 8 4 5
Al dejar de mirar la secuencia, ¿cuántos dígitos puede recordar? En promedio, las personas pueden
retener y repetir unos 7 dígitos.La mayoría de los problemas abarcan muchos más ítems de información. Otro punto fundamental para hallar la solución de un problema es seleccionar los elementos de información que resulten relevantes.
La información puede ir organizándose en bloques, de manera tal de ir creando una clasificación. Por ejemplo, ítems tales como manzanas, naranjas e higos pueden agruparse en frutas. Frutas, verduras y carnes pueden conformar la clase comidas frescas. Las comidas frescas junto con los embutidos y conservas pueden agruparse en comidas, y así siguiendo. El agrupar ítems ayuda a retener y manipular más información. Para comprobarlo, agrupe de a tres dígitos la secuencia anterior e intente nuevamente retener los números formados. En el estudio de la lengua, se recurre frecuentemente a la frase El mi tu-te mas si se-de para agrupar a todos los monosílabos que pueden acentuarse o no 4 Evidentemente, es muy fácil recordar esta oración, aún cuando no tiene sentido, en lugar de memorizar las 8 palabras aisladamente. Frecuentemente resulta útil desarrollar patrones que incluyan ítems aparentemente sin relación. Los diagramas, los gráficos y las ecuaciones son ejemplos de herramientas que permiten condensar información.
5.1. Abstracción
El primer paso en la búsqueda de la solución es encontrar una representación adecuada para el problema, que descarte la información superflua y rescate aquélla que resulte relevante. La técnica para encontrar un planteo más conciso del problema se conoce como abstracción. Una abstracción de esta clase se realiza en varias etapas:
Los problemas normalmente se plantean en forma verbal. Antes de encontrar otra forma de representación, es conveniente probar con una nueva versión más sucinta del problema original. Por ejemplo: eliminar redundancias, datos irrelevantes y puntualizar el resto en frases cortas y claras.
Transformar el enunciado original en uno tan simple como sea posible. La nueva versión no necesariamente será más corta que la original.
Leer detenidamente el enunciado, y resaltar las
frases más importantesy tacharaquellas que no sean relevantes.Identificar los objetos relevantes y las relaciones entre estos objetos.
Agrupar los objetos en clases.
Nombrar los objetos o las clases según alguna notación adecuada.
Definir las operaciones que pueden aplicarse sobre los objetos.
Utilizar, siempre que sea posible, una notación más abstracta que una descripción verbal.
El objetivo de la abstracción es construir una simplificación de la realidad que rescate únicamente la información relevante para hallar la solución del problema. Intentamos construir un modelo de la realidad. Un modelo es, precisamente, una representación simplificada de la realidad. La construcción de un modelo es útil porque sólo son considerados los elementos relevantes y así la búsqueda de la solución no se ve entorpecida por el exceso de detalles.
5.2. Diagramas
Una de las reglas heurísticas más aplicadas consiste en confeccionar figuras de análisis: Diagramas, esquemas, tablas, mapas, etc. Ellos nos perimten organizar la información y nos ayudan en el proceso de búsqueda de soluciones, y a encontrar los medios para resolver los problemas.
Existen muchos problemas en los que resulta adecuado encontrar una representación gráfica de los mismos.
Ver video sobre la ultización de Diagramas de Venn en la resolución de Problemas: [https://youtu.be/a3cD1O44G8Q]
Ejemplo 5.5 Un hombre y una mujer caminan juntos. En el momento inicial sus pies derechos
están apoyados en el suelo. El hombre da 2 pasos por cada 3 de la mujer. ¿Cuántos pasos deben
dar cada uno antes de que sus pies izquierdos pisen el suelo simultáneamente?Ejemplo 5.6 Blanca, Rosa y Violeta son tres amigas que se encuentran para estudiar y descubren
que, casualmente, están vestidas con los colores de sus nombres, aunque ninguna lleva el color que
corresponde al su nombre. Si el vestido de Violeta no es blanco, ¿cuál es el color de los vestidos de
cada amiga?Intentemos ahora aclararlo en un cuadro de doble entrada. En el mismo ya está indicado, con una letra mayúscula la inicial del nombre de cada amiga y con una letra minúscula el color de cada vestido. Coloque una cruz en aquella intersección que resulte falsa a los datos que se le dieron y un círculo cuando resulte verdadera
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | ? | ? | ? |
| rosa | ? | ? | ? |
| violeta | ? | ? | ? |
Vea la resolución paso a paso de este ejercicio haciendo click en la flechita negra:

Ejercicio 5.6
Objetivo: Conocer cuál es el color de los vestidos de cada amiga.
Los nombres de las tres amigas son: Blanca, Rosa y Violeta.
Descubren que están vestidas con los colores de sus nombres.
Ninguna lleva el color que corresponde al su nombre.
El vestido de Violeta no es blanco,
Estrategia. Diagramas. Construimos una tabla de doble entradas. En columnas representamos a las amigas, por eso cada columna está etiquetada con cada nombre. Las filas representan los colores de los vestidos:
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | ? | ? | ? |
| rosa | ? | ? | ? |
| violeta | ? | ? | ? |
Desarrollo: Como ninguna lleva el color que corresponde a su nombre:
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | ? | ? |
| rosa | ? | X | ? |
| violeta | ? | ? | X |
Luego, debido a que el vestido de Violeta no es blanco,
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | ? | X |
| rosa | ? | X | ? |
| violeta | ? | ? | X |
Luego inferimos que la única posibilidad para Violeta es que use un vestido color Rosa.
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | ? | X |
| rosa | ? | X | o |
| violeta | ? | ? | X |
Luego, indicamos el vestido rosa ya esta asignado
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | ? | X |
| rosa | X | X | o |
| violeta | ? | ? | X |
Luego, Blanca usa el violeta:
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | ? | X |
| rosa | X | X | o |
| violeta | o | ? | X |
Finalmente, deducimos que Rosa usa el blanco
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | o | X |
| rosa | X | X | o |
| violeta | o | X | X |
Violeta usa el vestido color rosa
Rosa usa el vestido color blanco
Blanca usa el vestido color violeta
| Blanca | Rosa | Violeta | |
|---|---|---|---|
| blanco | X | o | X |
| rosa | X | X | o |
| violeta | o | X | X |

Verificación, en este caso hay que tomar la tabla final
Y verificar que se cumplen las restricciones
Ninguna lleva el color que corresponde al su nombre.
El vestido de Violeta no es blanco,
5.3. Matemáticas
Una de las características más interesantes de usar herramientas matemáticas como forma de representación es su rigidez y formalidad. Esto asegura que si se obtiene una expresión adecuada y se obedecen bien las reglas, es posible llegar a una solución acertada, independizándose rápidamente del enunciado original. La Matemática nos ofrece técnicas muy variadas para modelar problemas, tales como ecuaciones, grafos, lógica, geometría y otras. La máxima ventaja de utilizar una herramienta matemática es la sólida teoría sobre la que se apoya y la independencia que se logra del enunciado original, una vez que el problema ha sido modelado.
5.3.1. Ecuaciones
Las ecuaciones parten de una serie de incógnitas que representan valores -desconocidos a priori- y una serie de símbolos u operadores que establecen relaciones entre las incógnitas. La solución consiste en ir estableciendo nuevas relaciones entre las incógnitas -usando las reglas del álgebra-, que permiten llegar a una expresión simple donde se haga conocido el valor para una de las incógnitas. Se puede continuar con este proceso hasta encontrar la solución del problema global. En este caso, el enunciado se transforma en ecuaciones en las que los objetos del problema son operandos y las relaciones entre los mismos son los operadores.
Ejercicio 5.4.1.: Clariobaldo es ahora tres veces más viejo de lo que lo era su sobrina Anabela hace 10
años y Anabela tiene ahora la mitad de la edad que tendrá su tío dentro de 5 años. ¿Cuánto más
viejo es Clariobaldo que Anabela?
Ejercicio 5.4.1
Determinar cuantos años más tiene Claribaldo respecto de Anabela.
Clariobaldo es ahora tres veces más viejo de lo que lo era su sobrina Anabela hace 10 años
Anabela tiene ahora la mitad de la edad que tendrá su tío dentro de 5 años.
Representación Matemática, Ecuaciones.
Siendo: C = edad de Claribaldo A = edad de Anabela
C = 3(A − 10) (1)
A = (C+5) / 2 (2)
Luego reemplazando la ecuación (1) en la ecuación (2) obtenemos:
A = ( 3(A − 10) +5) / 2
A = ( 3A − 30 +5) / 2
2A = 3A − 30 +5
30-5 = 3A -2A
25 = A
Luego por (1):
C = 3(A − 10) = 3(25 − 10) = 3(15)= 45
Claribaldo tiene 20 años más que Anabela.
Verificación: C = 3(A − 10) (1)
45= 3(25 -10) 45 = 3(15) 45 = 45
A = (C+5) / 2 (2) 25 = (45+5) /2 25 = 50/2 25 = 25

En ejercicio anterior los conceptos relevantes son las edades de Clariobaldo y Anabela y la relación entre estas edades. Una primera simplificación asigna nombres a las edades. En segundo término, la relación entre las edades puede expresarse fácilmente a través de ecuaciones algebraicas.
En el ejercicio hemos encontrado una representación equivalente, mucho más expresiva. Para hallar la solución, a su vez podemos limitarnos a las ecuaciones planteadas, descartando el enunciado original. En cualquiera de los casos anteriores, la idea fue pasar de un enunciado planteado verbalmente a una expresión más sucinta, consistente de operadores y operandos. A partir de dichas expresiones, llegamos a la solución, usando las reglas del álgebra. En el ejercicio anterior podemos establecer que el paso más abstracto y representativo fue saltar del enunciado a la ecuación. Alli hemos puesto toda nuestra creatividad. A partir de este planteo, nos hemos independizado casi del problema y hemos operado en forma genérica.
Podes descargar la plantilla en formato word en este enlace: [http://opendata.fi.uncoma.edu.ar/Plantilla.docx]
Mostramos a continuación dos problemas más para practicar. Utilizá una hoja para resolver el primer item de la plantilla y luego de resolverlo, compará con la solución.
Dados
Se arrojan tres dados, sabemos que la suma de los tres dados es 11, la suma del primero y el tercero 5 y el segundo es el doble el tercero.¿Qué número salió en cada dado?
Ej Dados de Teoría
Objetivo: Conocer que número salió en cada dado.
La suma de los tres dados es 11
La suma del primero y el tercero es 5
El segundo es el doble del tercero
Matemática Ecuaciones. x es el primer dado, y es el segundo dado, z es el tercer dado
x + y + z = 11 (1)
x + z = 5 (2)
y = 2 Z (3)
Desarrollo: si despejamos de la ecuación 2 la variable x obtenemos
x + z = 5 (2)
x= 5 - z
Esta ecucación que obtenemos y la ecuación 3, la utilizamos en la ecuación 1, asi todo nos queda en un función de una sola variables (z):
x + y + z = 11 (1)
(5-z) + 2 z + z = 11
5 -z +2z +z = 11
2z = 11 -5
2z = 6
z = 6/2
z = 3
Si z = 3, debido a que y = 2z entonces y = 6
Si z= 3, debido a que x = 5-z entonces x = 2
El tercer dado muestra la cara 3;
el segundo dado (Y) muestra la cara 6;
el primer dado (x) muestra la cara 2.
Verificamos las tres ecuaciones:
x + y + z = 11
2 + 6 +3 = 11
11 = 11x + z = 5
2 + 3 = 5
5 = 5
y = 2 Z
6 = 2 * 3
6 = 6

Padre e Hijo:
Alberto y su padre se llevan 25 años de edad.
Calcular la edad de Alberto sabiendo que dentro de 15 años la edad de su padre será el doble que la suya.
Ejercicio Padre e hijo
Objetivo: Conocer cuál es la edad de Alberto
Alberto y su padre se llevan 25 años de edad.
dentro de 15 años la edad de su padre será el doble que la suya.
Matemática, Ecuaciones. a será la veriable que representa a Alberto, y p la variable que representa a su padre
p = a + 25 (1)
(p+15) = 2 (a+15) (2)
Remplazando ecuación 1 en 2 obtenemos:
(p+15) = 2 (a+15)
((a+25) + 15) = 2 (a+15)
Luego
a + 40 = 2a + 30
40 -30 = 2a -a
10 = a
si a = 10 entonces como p= a + 25 luego p= 35
Alberto tiene 10 años y su padre 35 años.
verificamos ambas ecuaciones:
p = a + 25
35 = 10 + 25
35 = 35
(p+15) = 2 (a+15)
35 + 15 = 2 (10 + 15)
50 = 20 + 30
50 = 50

5.3.2. Lógica
La lógica define muy precisamente el significado de ciertas expresiones y de algunos conectivos como y, o, si-entonces. La lógica maneja valores de verdad. Si una afirmación simple es conocida como verdadera o falsa, entonces la lógica puede determinar si una afirmación compuesta, que involucra afirmaciones simples, es verdadera o falsa. Por ejemplo, suponiendo que disponemos de dos afirmaciones simples: ’Yo soy un hombre’ ’Yo tengo 30 años’
que se saben verdaderas, la afirmación ’Yo soy un hombre y yo tengo 30 años’ es también verdadera. Está claro que si alguna de las afirmaciones fuera falsa, entonces la afirmación compuesta sería también falsa. El problema de la lógica consiste en establecer la verdad de ciertas afirmaciones iniciales o de partida. Estas asignaciones caen bajo la órbita humana y, por tanto, el sistema muchas veces es peligroso. Por ejemplo, si partimos de la verdad de las siguientes afirmaciones: ’Todos los venenos son ácidos’. El arsénico no es ácido’. Entonces podemos deducir que el arsénico no es un veneno. Claramente, esto es falso. El problema ha sido la asignación inicial de verdadera para la primera afirmación. Esto no implica que la lógica no sirva, sino que es necesario tener mucho cuidado al establecer los valores de verdad para ciertas afirmaciones.
5.3.3. Grafos
Un grafo es una representación pictórica que consiste en una serie de círculos o nodos y una serie de líneas aristas que vinculan los nodos. Los aristas pueden estar nombradas o etiquetadas de modo de indicar su propósito ó cómo pasar de un nodo a otro. Un grafo puede usarse para representar gran variedad de problemas, siempre y cuando el número de situaciones a considerar sea finito. Si las aristas estan orientadas estas pasan a denominarse arcos, y el grafo se transforma en un digrafo.
Ejemplo 5.8 Supongamos que un viajante debe organizar su próxima gira a distintas ciudades de
la provincia de Neuquén (Neuquén, San Martín de los Andes, Villa la Angostura, Copahue, Zapala y Junín de los Andes), partiendo del kilómetro 0 en la Ciudad de Buenos Aires. Construir un grafo donde los nodos son ciudades y los arcos son las distancias entre las mismas.
Determinar el circuito, el camino más óptimo para el viajante.Considerando la siguiente tabla de distancias entre ciudades:
| Ciudades | Copahue | Junín de los Andes | Neuquén | San Martín de los Andes | Villa La Angostura | Zapala |
|---|---|---|---|---|---|---|
| Copahue | al Km 0: 1545 | 373 | 375 | 414 | 522 | 202 |
| Junín de los Andes | 373 | al Km 0: 1561 | 347 | 41 | 149 | 208 |
| Neuquén | 375 | 347 | al Km 0: 1166 | 423 | 477 | 182 |
| San Martín de los Andes | 414 | 41 | 423 | al Km 0: 1602 | 110 | 241 |
| Villa La Angostura | 522 | 149 | 477 | 110 | al Km 0: 1770 | 351 |
| Zapala | 202 | 208 | 182 | 241 | 351 | al Km 0: 1355 |
Podemos construir un grafo en el cual los nodos son las ciudades y los arcos están etiquetados con las distancias entre aquellas ciudades que une el arco.
No obstante el grafo no es suficiente. Tenemos restricciones que son las rutas que unen las ciudades. Sabemos que desde Neuquén podemos llegar a Villa la Angostura pasando por San Martín de los Andes, o sin pasar por San Martín de los Andes. Además conocemos que Junín de los Andes está muy cerca de San Martín de los Andes. Teniendo en cuenta el siguiente mapa con las rutas mas importantes es posible simplificar el grafo anterior para encontrar el camíno óptimo.
Encontraremos una representación abstracta para un problema concreto. Esta representación se apoya en la teoría de grafos, que será vista en materias posteriores. Mediante el uso de esta técnica, será posible encontrar el camino mínimo uniendo todas las ciudades. Si hemos obedecido bien las reglas de grafos, sabremos que el camino obtenido es el mínimo y no habrá dudas al respecto.
5.3.4. Geometría
La geometría brinda una herramienta visual a la cual se le pueden aplicar ciertas leyes, conocidas, en la búsqueda de la solución. La ventaja de llevar un problema a una representación que se apoye fuertemente en una teoría, permite abstraerse rápidamente del problema y hallar la solución usando un método genérico
Debemos distinguir el perímetro del area de una figura geométrica.
CUADRADO
Área: \(A\) = \(a^2\)
Perímetro: \(P\) = \(4a\)
RECTÁNGULO
Perímetro: \(P\) = \(2b+2h\)
Área: \(A\) = \(b*h\)
CÍRCULO
Perímetro: \(P\) = \(d\) \(\Pi\)
Área: \(A\) = \(\Pi\) \(r^2\)
El apunte titulado ’Ayuda para Resolver Problemas’:Enlace al apunte contiene la fórmulas más comúnmente utilizadas en distintas figuras geométricas.
Con cualquiera de los conceptos matemáticos que hemos presentado, encontrar un modelo matemático adecuado nos permite utilizar toda la teoría desarrollada y probada para el modelo. De todos estos conceptos el único que resulta conocido hasta el momento es probablemente el de ecuaciones algebraicas. Notemos que una vez hallado un conjunto de ecuaciones para representar el planteo de un problema, hallamos la solución siguiendo las reglas y propiedades del álgebra. Como lo correcto de estas reglas y propiedades está asegurado por una teoría, no necesitamos comprobar la validez de los resultados. Por el momento, no podemos mostrar que lo mismo ocurre cuando utilizamos grafos o lógica, precisamente porque desconocemos la teoría que soporta a estos conceptos y serán vistos en otras materias. Podemos encontrar distintas representaciones, algunas de ellas son mejores que otras, según el tipo de problema. En cualquier caso, el punto notorio e importante es la identificación de los objetos relevantes del problema, las relaciones entre ellos, sus propiedades y otras características que constituirán los datos del problema
6. Resumen
En la siguiente figura podemos observar un mapa conceptual que describe la estructura de este documento.
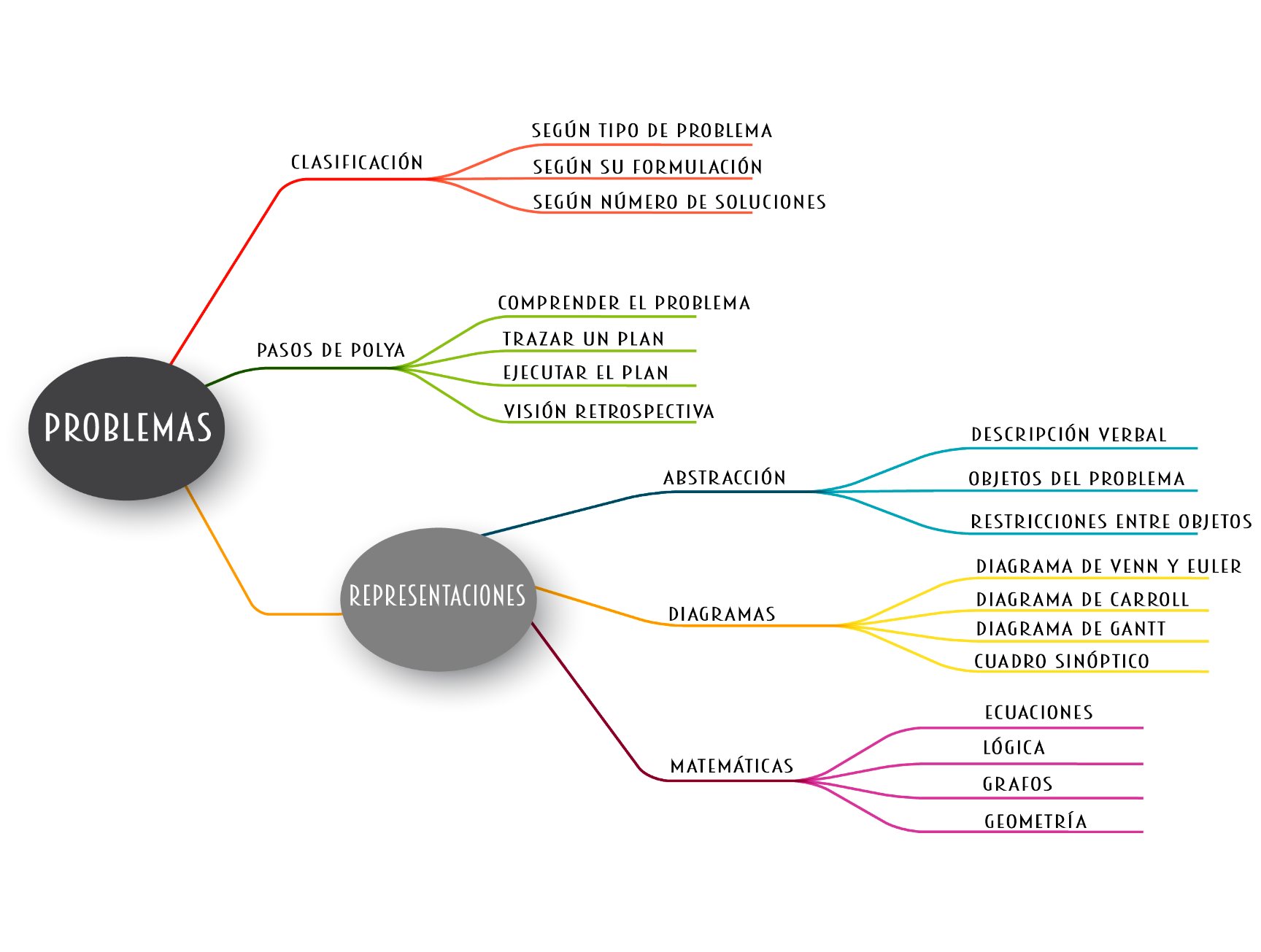
7. Referencias
Broadbent, D. E. (1975). The Magical Number Seven after Fifteen Years. In A. Kennedy and A. Wilkes (eds.), Studies in Long-Term Memory, New York: Wiley, pages 3–18.
Gopal, R. (1991). Dynamic Program Slicing Based on Dependence Relations. Proceedings of the Conference on Software Maintenance, pages 191–200.
Miller, G. A. (1956). The Magical Number Seven, Plus or Minus Two: Some Limtis on our Capacity for Processing Information. Psycological Review, 63:81–97.
Polya, G. (1965). Mathematical Discovery: On Understanding, Learning and Teaching Problem Solving. John Wiley and Sons.
Polya, G. (1973). How to Solve it, A New Aspect of Mathematical Method. Princeton University Press. Princeton, New Jersey.
Reynoso, L., Rodriguez, J., Sanchez, L., and Alvarez, M. (2012). A Collaborative Management Model in Learning and Teaching Process (collMMod-LTP): An application for Problem Solving and Algorithms. Proc. IEEE 11th International Conference on Cognitive Informatics Cognitive Computing (ICCI*CC 2012), pages 448–455.
UNComahue (2020). Ayuda para Resolver Problemas. Apuntes de la Cátedra de Resolución de Problemas y Algoritmos. Facultad de Informática.
8. Videos clases anteriores
- Primera clase, año 2022: [https://youtu.be/IqWp9zNXmDU]
- Primera clase, año 2021: [https://youtu.be/4qmExOfQY48]
- Segunda clase, año 2021, módulo 1: [https://youtu.be/pCwD6akdAWs]
- Segunda clase, año 2021, módulo 2: [https://youtu.be/tIr0XeWD4hY]






